Crystallography
Crystal Systems
A crystal system is one of the various classifications of crystals, lattices, and space groups. Crystal system and lattice system terms are related but have a slight difference in crystallography.
Crystals are categorized into general types based on their forms. A crystal is defined by its faces, which connect at precise angles and are unique to the given substance. The geometrical form and symmetry of the crystal systems are used to name the crystal systems. The seven crystal systems are as follows:
These seven crystal systems are detailed below, with an example of each. A crystal’s edge lengths are symbolized by the letters a, b, and c. The Greek letters are α, β, and γ used to indicate the angles at which the faces connect. The angles between the faces and the number of equal-length edges on each face vary between the seven crystal systems.
Bravais Lattices
In crystals, atoms can be organized into one of 14 possible three-dimensional patterns, which is known as the Bravais lattice. The smallest collection of atoms with symmetrical alignment that can be repeated in an array to form the full crystal is referred to as a unit cell. A Bravais lattice is, to put it simply, a collection of discrete points that are arranged and oriented in such a way that they are all indistinguishable from one another from any other discrete point. Based on the properties of the cells, these 14 lattices are grouped into seven crystal systems. Bravais lattices are classified as primitive, body-centered, face-centered, and base-centered.
All the unit cell edge lengths are equal and perpendicular to one another in this crystal structure. The connection may be seen as follows:
a = b = c
α = β = γ = 90°
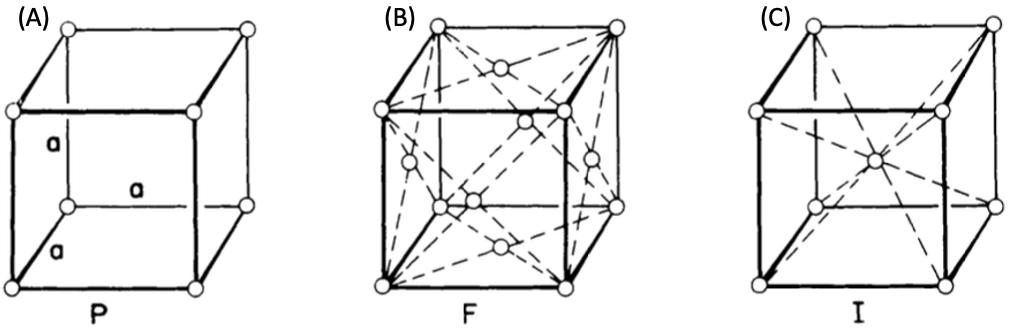
Figure 1. Cubic systems as simple cubic (A), face-centered cubic (B), and body-centered cubic (C) crystal structures.
It follows that a Bravais lattice with cube-like symmetry is the most symmetrical. These three unique lattice types—simple (primitive) (P), face-centered (F), and body-centered (I)—are used in this system. Silver, garnet, gold, and diamond are a few examples of cubic systems.
-
-
In simple cubic, lattice points or atoms are present at the corners of the cube. Simple cubic is an uncommon crystal structure due to its atom’s positions, angles of the edges, and its relatively low packing density. Polonium is one of the only materials that have a simple cubic crystal structure.
-

Figure 2. The element of Polonium is a highly radioactive material. It was discovered in 1989 owing to its highly radioactive nature.
-
In the face-centered cube, atoms are found at corners and at the centers of all faces of the cube. Face-centered cubes are common because they have a very high packing density as a crystal structure. Nickel and copper, elements are the most well-known examples of elements with this crystal structure.

Figure 3. Nickel (A) and copper (B) materials.
-
In the case of a body-centered cube, atoms are present at the corners, and one atom is completely present at the center of the cube (Figure 1. (C)). Because of its high packing density, body-centered cubic crystals are widespread. Iron and tungsten elements are the most well-known examples of elements with this crystal structure.

Figure 4. Iron (A) and tungsten (B) materials.
The unit cell edges in this crystal structure have two edges that are the same length and one edge that has a different length. Each of the three edges is perpendicular to the others. The relationship can be observed as follows:
a = b ≠ c
α = β = γ = 90°
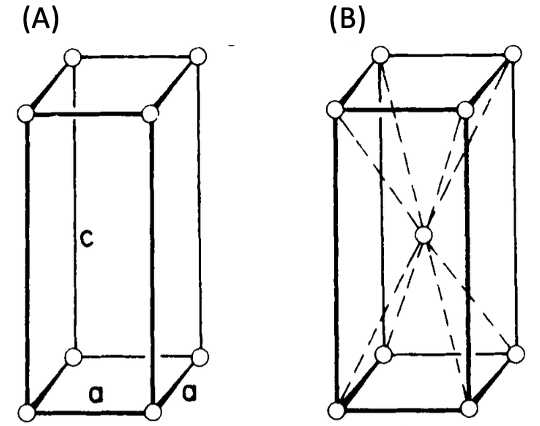
Figure 5. Tetragonal systems as (A) simple, (B) body-centered tetragonal crystal structures.
The tetragonal system has two Bravais lattices. They are simple tetragonal cells (Fig. 5(A)) and body-centered tetragonal cells (Fig. 5(B)), as shown above. Examples of tetragonal systems are tin oxide as a simple tetragonal and titanium dioxide as a body-centered tetragonal.

Figure 6. Cassiterite (stannic oxide) (A), titanium dioxide (B) crystals.
The unit cell’s two edges in this crystal structure have equal lengths on both sides and a 120° angle between them. These two edges are not equal in length and are perpendicular to the third edge. The relationship can be observed as follows:
a = b ≠ c
α = β = 90°; γ = 120°.
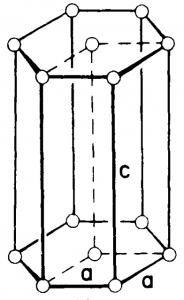
Figure 7. Hexagonal crystal structure.
The Bravais lattice is primitive only. This is shown in Figure 7. In this crystal formation, the atoms are organized in a hexagonal close packing. Simple hexagonal unit cells are the building blocks of beryllium oxide and zinc oxide.

Figure 8. Colored scanning electron microscope image of zinc oxide (A) and beryllium oxide (B).
In an orthorhombic crystal system, unit cell edge lengths are different, and they are perpendicular to one another. The relationship can be observed as follows:
a ≠ b ≠ c
α = β = γ = 90°
This system has four Bravais lattices. They are simple, base-centered, face-centered, and body-centered. These are shown in Figure 9. Examples of orthorhombic crystal systems are K2SO4, SnSO4, etc.
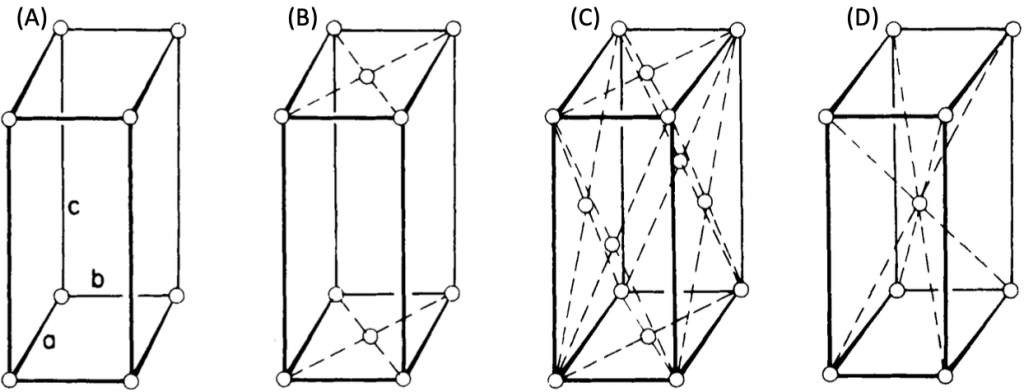
Figure 9. Orthorhombic crystal systems: simple (A), base-centered (B), face-centered (C), body-centered (D) orthorhombic crystals.
-
Simple orthorhombic crystals are often more stable than monoclinic or triclinic crystal structures, although they are not as stable as cubic crystals. The crystal structures of gallium, phosphorus, and bromine are orthorhombic.
-
There are several minerals with crystal structures that have an underlying Bravais lattice that is base, face, and body-centered orthorhombic, but no elements with these three types of crystal structures. Some examples of minerals are epsomite, marcasite, aragonite, olivine, etc. (Fig. 10.).

Figure 10. Minerals in the orthorhombic crystal structure are epsomite (A), marcasite (B), aragonite (C), and olivine (D).
At the Rhombohedral crystal system (also can be called “Trigonal”), all three axes are of equal length, and all the axes are at the same angle to another, but none of them is perpendicular. The connection may be seen as follows:
a = b = c
α = β = γ ≠ 90°
The symmetry of a rhombohedron, shown in Figure 11, can be created by extending or compressing a cube along one of its spatial diagonals without altering the length of the edges. There is only a “simple” rhombohedral since extra atoms on the faces or center are not possible.
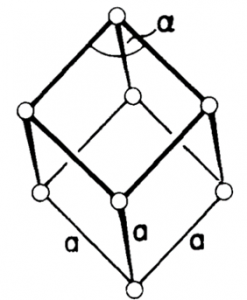
Figure 11. Rhombohedral crystal structure.
Mercury, antimony, and bismuth are a few low-melting-point elements that have rhombohedral crystal structures. Rhombohedral unit cells are also the building blocks of selenium, calcite, and sodium nitrate.

Figure 12. Selenium (A), Calcite (B), and sodium nitrate (C).
Crystals in this system are referred to as all three axes of unequal lengths, and two axes are perpendicular to each other, but the third axis is not perpendicular to the other two axes. The connection may be seen as follows:
a ≠ b ≠ c
α ≠ 90, β and γ = 90˚
Monoclinic has a poor symmetry, such as that in figure 13, which was created by “slanting” a rectangular parallelepiped along one edge to create a right parallelepiped with any base. This system includes two Bravais lattices, simple (Fig. 13 (A)) and base-centered (Fig. 13 (B)).
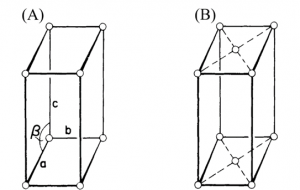
Figure 13. The monoclinic system is (A) simple, (B) base-centered monoclinic crystal structures.
Gypsum, β-sulfur, borax, azurite, kaolin, orthoclase, muscovite, clinopyroxene, jadeite, and spodumene crystallize in the monoclinic system.

Figure 14. Gypsum (A), β-sulfur (B), borax (C), and azurite (D) are structured in a monoclinic crystal structure.
Crystals in triclinic systems are referred to three axes of unequal lengths that are inclined at three different and non-perpendicular angles relative to each other. This corresponds to the symmetry of an arbitrary oblique parallelepiped. The connection may be seen as follows:
a ≠ b ≠ c
α ≠ β ≠ γ ≠ 90˚
It is the lowest symmetry, comprising only a center of symmetry. It includes only one Bravais lattice simple.
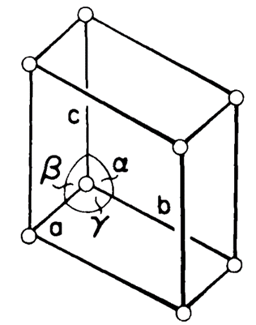
Figure 15. Triclinic crystal structure.
There are no elements that have a triclinic crystalline structure. However, certain minerals, including turquoise and microcline, have crystal structures with a triclinic.

Figure 16. Minerals in the triclinic crystal structure; turquoise (A) and microcline (B).
Sources:
M. J. Mehl, D. Hicks, C. Toher, O. Levy, R. M. Hanson, G. L. W. Hart, and S. Curtarolo. The AFLOW Library of Crystallographic Prototypes: Part 1. Comp. Mat. Sci. (2017). 136, S1-S828. (doi=10.1016/j.commatsci.2017.01.017)
D. Hicks, M. J. Mehl, E. Gossett, C. Toher, O. Levy, R. M. Hanson, G. L. W. Hart, and S. Curtarolo. The AFLOW Library of Crystallographic Prototypes: Part 2. Comp. Mat. Sci. (2019). 161, S1-S1011. (doi=10.1016/j.commatsci.2018.10.043)
Tin Oxide Materials Synthesis, Properties, and Applications 1st Edition – October 1, 2019, Editor: Marcelo Ornaghi Orlandi.
M. Pitteri and G. Zanzotto. “On the Definition and Classification of Bravais Lattices”. Acta Cryst. (1996). A52, 830-838. (doi=10.1107/S0108767396005971)
L. D. Landau, A. I. Akhiezer, E. M. Lifshitz. General Physics: Mechanics and Molecular Physics. Kindle Edition.
Britannica. “Monoclinic System”. Access: 5 March 2023. https://www.britannica.com/science/monoclinic-system
W. D. Callister, Jr. D. G. Rethwisch. “Materials Science and Engineering an Introduction”. Eight Edition. Publisher: John Wiley and Sons. (2009)
Periodic Table. “An example of the element Selenium”. Access: 5 March 2023. https://periodictable.com/Items/034.4/index.html
J. Sinkankas. Mineralogy for amateurs. Van Nostrand. (1964). pp. 359–364.
Chemistry Learner. “Sodium Nitrite”. Access: 5 March 2023. https://www.chemistrylearner.com/sodium-nitrite.html
Flickr. “Monoclinic Sulfur”. Tanaka, R. Access: 5 March 2023. https://www.flickr.com/photos/fluor_doublet/2248805914/in/photostream/
